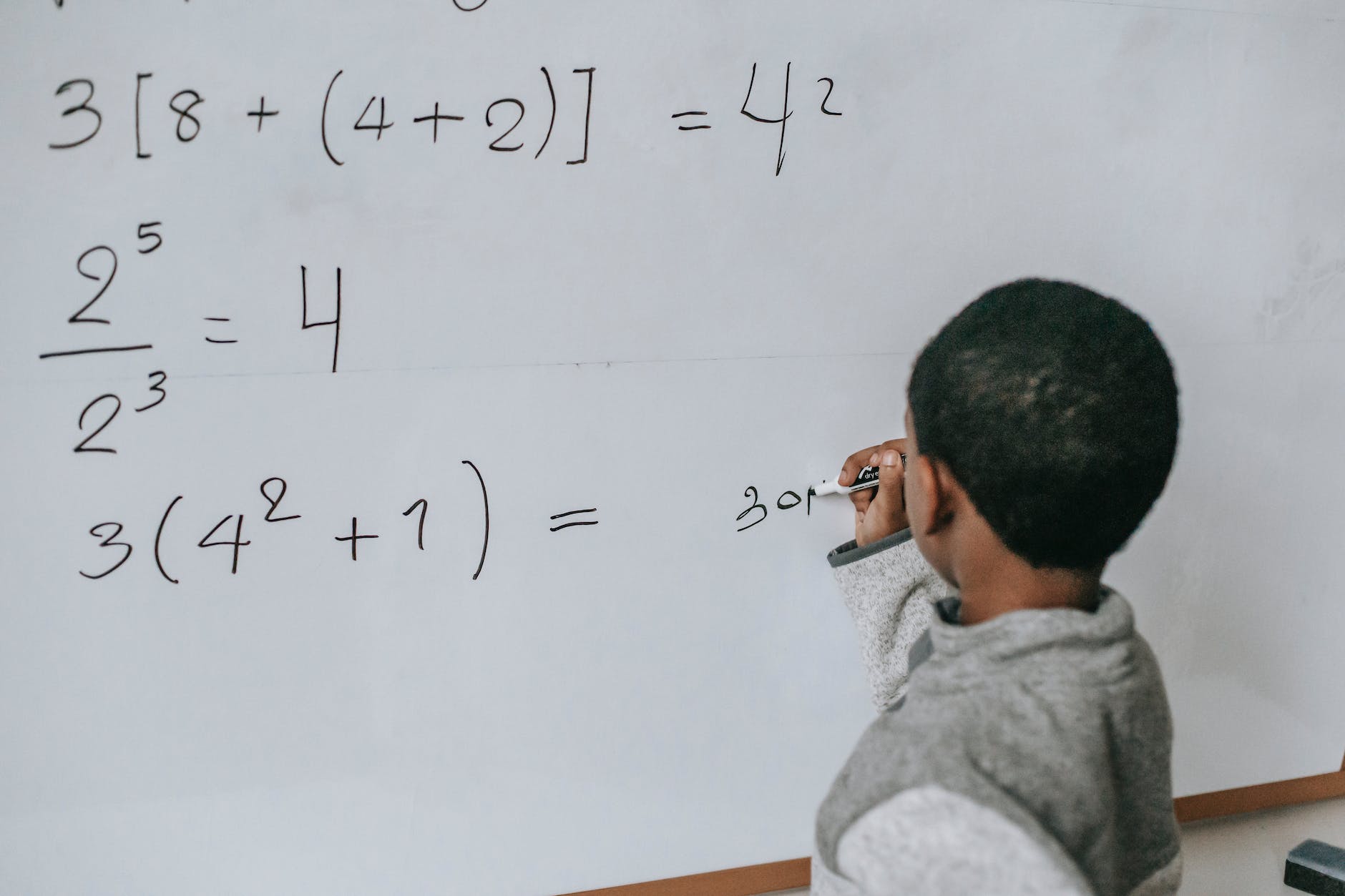
A quick review of P.E.M.D.A.S. (PEMDAS) reminds us that it is an acronym for the order of operations rules. Namely, Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. This time, we will take a deeper look at the second problem on the board. It contains Exponents (Multiplication) and a fraction which is Division. If you know how Exponents as fractions are solved, you are aware it also contains Subtraction.
The problem appears straight-forward; however, the fraction adds an additional step. When the foundation of PEMDAS is learned and easily accessible in a student’s skill set, the Exponent/Fraction concept will be easily understood.
Identification
We start with identification of the terms:
- Numerator: Coefficient-2, Exponent – 5
- Denominator: Coefficient-2, Exponent –3
This problem expresses a value using Exponents as a fraction. An Exponent is the number of times a number, called a coefficient, is multiplied by itself. A fraction is a representation of part(s)/of a whole. The numerator lists the parts and the denominator is the whole value. This problem is being used to show the concept of how to simplify Exponents as fractions.
Concept
While solving the exponents first is one path to the solution ( 2 5=32/23=8; 32/8=4), that process is cumbersome with larger exponents. The concept for solving exponents as fractions states, if the co-efficients are the same – as they are in this problem, the numerator is the power and the denominator is the root. The solution is accomplished using subtraction to complete the division. First, find the smaller exponent in the denominator (“3”) and subtract it from itself. Next, subtract the denominator “power” (“3”) from the numerator “power” (5″). The division is accomplished by subtracting the denominator root from itself and from the numerator power.
Solution
It is as simple as:
25 /23 – becomes 2 5-3 / 23-3 when you solve the subtraction, you have 22 /20 which simplifies to 22/1.
Thus illustrating the zero-power concept (20). Any number raised to the power of zero is 1. Finally, solve the exponent by multiplying 2×2=4. The same answer the student recorded.*More examples
Summary
In summary, Exponents as fractions seem scary until you understand what to do with them. It is, also, an exercise in pattern recognition. Mental math resources for the subtraction and multiplication portions will make calculations faster. Students who have solid mental math skills are more confident and able to understand concepts better. If your student takes the time to build or re-build an unstable mental math foundation, It is the best and fastest way to concept comprehension. Contact me – I CAN help. Until next time. dream BIG and let your D.R.E.A.M.S. take you there!
Next: Problem #3